2025년 6월 2일 수정
서까래 각도를 어떻게 구할 수 있을까요?
건물 지붕을 보면, 위로 뾰족하게 올라간 삼각형 모양이 많습니다. 이때, 지붕의 기울기나 각도를 구하고 싶을 때는 삼각형의 성질과 수학을 사용하면 알 수 있어요.
1. 삼각형과 각도
삼각형에는 세 개의 변과 세 개의 각이 있어요. 변의 길이를 알면, 각도를 구할 수 있어요.
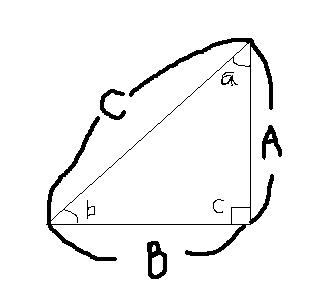
- 변 A: 바닥에 해당하는 가로 길이
- 변 B: 세로로 올라간 높이
- 변 C: 지붕의 경사면 길이 (빗변)
이런 삼각형에서는 ‘삼각함수’라는 걸 이용해서 각도를 구해요.
2. 각도를 구하는 방법
삼각함수를 이용하면 각도를 구할 수 있어요. 아래는 변의 길이로 각도를 계산하는 방법입니다.
- cos(각도) = 밑변 ÷ 빗변 = A ÷ C
- sin(각도) = 높이 ÷ 빗변 = B ÷ C
- tan(각도) = 높이 ÷ 밑변 = B ÷ A
그런데 우리가 알고 싶은 건 ‘각도’죠?
그래서 위 공식을 거꾸로 써야 해요. 이걸 역삼각함수라고 해요.
예를 들어:
- arccos(B ÷ C) 는 B와 C의 길이를 알 때 각도를 알려줘요.
- arctan(B ÷ A) 도 마찬가지예요.
3. 예를 들어 볼게요!
- 빗변 C = 5
- 높이 B = 3
- 밑변 A = 4
이때 각도를 구해볼게요.
- cos(각도) = A ÷ C = 4 ÷ 5 = 0.8
- 각도 = arccos(0.8) 계산기로 누르면 약 36.87도가 나와요!
4. 더 정확하게 계산하고 싶다면?
수학자들은 이 각도를 계산기로만 구하지 않고, 수식으로도 계산할 수 있게 해놨어요. 예를 들어, arctan(x)는 다음과 같은 식으로 계산할 수 있어요.
arctan(x) = x - x³/3 + x⁵/5 - x⁷/7 + ...이렇게 계속 더하고 빼면서 점점 더 정확한 값에 가까워져요. 단, 이건 고등학교에서 배우는 내용이라, 지금은 ‘이런 방법도 있다’ 정도로만 알아두면 좋아요.
5. 마무리
- 지붕 각도는 삼각형의 변을 이용해 구할 수 있어요.
- 삼각함수와 역삼각함수를 이용하면, 변의 길이로 각도를 계산할 수 있어요.
- 계산기로 arccos, arcsin, arctan 같은 버튼을 사용하면 쉽게 각도를 알 수 있어요.
Q&A
❓ Q1. 서까래 각도는 왜 구해야 하나요?
👉 지붕을 만들 때 각도가 너무 작으면 비가 잘 안 빠지고, 너무 크면 재료가 더 많이 필요해요.
적당한 각도를 정해서 튼튼하고 효율적인 지붕을 만들기 위해 각도를 구해야 해요.
❓ Q2. 삼각형의 세 변 중 어떤 걸 알아야 각도를 구할 수 있나요?
👉 두 개의 변만 알아도 각도를 구할 수 있어요!
예를 들어, 밑변(A)과 빗변(C)을 알면 cos(각도) = A ÷ C를 이용해 각도를 구할 수 있어요.
❓ Q3. ‘arccos’, ‘arctan’ 같은 건 뭔가요?
👉 이건 각도를 구하는 함수예요.
예를 들어 arccos(0.8)은 “cos값이 0.8일 때, 그 각도는 몇 도인가요?“를 뜻해요.
계산기에서 이 함수들을 사용할 수 있어요.
❓ Q4. 각도는 항상 ‘도’로 나오는 건가요?
👉 아니요. **수학에서는 보통 ‘라디안’(rad)**이라는 단위를 써요.
하지만 일상에서는 ‘도(°)’를 더 많이 쓰기 때문에, 계산기에서 각도 모드를 ‘도’로 바꾸면 우리가 아는 30도, 45도처럼 나와요.
❓ Q5. 각도를 더 정확하게 구하는 방법도 있나요?
👉 네! arctan(x) = x – x³/3 + x⁵/5 – … 같은 수식으로 아주 정밀하게 계산할 수 있어요.
하지만 이런 계산은 고등학교나 대학교에서 배우는 거예요.
지금은 계산기만 잘 써도 충분히 정확하게 구할 수 있어요!
서까래 각도를 구하려고 합니다만…..
삼각함수의 역함수를 알면 저 각을 구할 수 있으며, 특수한 경우를 제외하고는 역함수를 써서 표현하는 것이 저 각을 ‘정확히’ 표현하는 유일한 방법입니다.
B/C = cos(b) = sin(a)
A/C = cos(a) = sin(b)
A/B = tan(b) = cot(a)
B/A = tan(a) = cot(b)
이므로,
b = arccos(B/C) = arcsin(A/C) = arctan(A/B) = arccot(B/A)
a = arcsin(B/C) = arccos(A/C) = arccot(A/B) = arctan(B/A)
입니다. 역삼각함수의 급수 전개는 잘 알려져 있으므로, 이를 이용하면 충분히 정확한 근사값을 얻을 수 있습니다. 가장 쉬운 급수 전개로, |x| < 1 일때 arctan x 을 급수로 전개하면
arctan x = x – x^3/3 + x^5/5 – x^7/7 + …
가 됩니다. 물론, 위에서 언급한 각의 단위는 모두 라디안입니다.